Measurement Uncertainty in Force Measurement

This article presents general ways of evaluating uncertainty in force measurement applications. It also applies this information to tolerances on load cell product specification sheets. The information in this article is from published journals and from related documents provided by the following standard bodies:
- European Association of National Metrology Institutes (EURAMET),
- National Institute of Standards and Technology (NIST), American Society for Testing and Materials (ASTM), and
- The Joint Committee on Guides in Metrology (JCGM).
The concept of uncertainty is somewhat new in measurement science. According to JCGM, as of 1977, there was no international consensus on the expression of measurement uncertainty [1]. This led the International Committee on Weights and Measures (abbreviated from the French, to CIPM) to have its sub-authority, the International Bureau of Weights and Measures (BIPM, again from French) collaborate with various national standard laboratories to derive this consensus. The resulting guidelines are applicable to a large spectrum of measurements, including force measurements [1].
This article includes the following topics:
- Measurement uncertainty in a load cell data sheet
- Misconceptions between error and uncertainty
- Standards procedures for estimating measurement uncertainty
- Lab procedures for determining force measurement uncertainty
- The importance of determining force measurement uncertainty
- Conclusion
Measurement Uncertainty In a Load Cell Data Sheet
Statistically Derived Uncertainty
The data sheet accompanying a strain gauge load cell specifies its output uncertainty as a percentage range of full-scale output (FSO). Assume the FSO is specified as \(2.2 mV/V \pm0.25\%\). Mathematically, this translates to \(2.2 mV/V \pm5.5 \mu{V}/V\) (since \(0.0025\) x \(2.2^{-3}=5.5^{-6}\)), or a range of \(2.1945 mV/V\) to \(2.2055 mV/V\).
To derive this uncertainty, ideally one would take repeated measurements using known masses and following nationally and internationally accepted procedures. The data set from these measurements would show the differences between this load cell’s outputs and expected measurement results. As explained later, these differences usually follow a Gaussian distribution around an expected value. The uncertainty value printed in the data sheet is generally two or three standard deviations above/below this expected value. In other words, when uncertainty is within two standard deviations, the load cell should give an output within this range with a confidence of 95%. Likewise, when uncertainty is within three standard deviations, the load cell output should be within the error boundaries with 99.7% confidence.
From this statistical evaluation, we know that the FSO for the specific load cell in this section will be in the range of \(2.1945 mV/V\) to \(2.2055 mV/V\) about 95% of the time, around a mean expected value of \(2.2 mV/V\). The \(5.5 \mu{V}/V\) in the first paragraph represents two standard deviations of the data of measurement samples. By the way, the number of standard deviations used to determine the confidence interval is also known as the coverage factor. This concept appears later in this article in more detail.
In Reality: a Word About Load Cell Classes
In reality, if every load cell underwent this type of testing, the cost would be prohibitive. Instead, standards bodies such as OIML and NIST set guidelines for the acceptable tolerances of various classes of load cell. Then manufacturers assign one of these classes to their load cells. This tells buyers which tolerance values apply to the load cell for the various parameters on its data sheets. Users can therefore expect output values of that load cell to fall withing those tolerances. But this is only true if ambient conditions, loading, mounting and maintenance are all per manufacturer’s guidelines. According to NIST, “Tolerance values are so fixed that permissible errors are sufficiently small that there is no serious injury to either buyer or seller of commodities, yet not so small as to make manufacturing or maintenance costs of equipment disproportionately high [8].”
You can read more about load cell classes in Load Cell Classes: OIML Requirements, and Load Cell Classes: NIST Requirements.
Misconceptions Between Error and Uncertainty
Often the terms “error” and “uncertainty” are used interchangeably. However their distinction is important. Measurement error is the difference between the observed value of a quantity and its actual value. Error is a theoretical concept that can never be truly known since it’s impossible to determine the actual value of a quantity. The article, Calibrating the Force Measuring System, explains various ways error is introduced to a measurement. Most of these ways are attributable to improper use of the measuring device or improper calibration. Therefore proper calibration methods can mitigate their effect.
Measurement error differs from measurement uncertainty. Error is a single value, while uncertainty is a range of measurement values that will occur with a probability known as the confidence interval. That is, uncertainty represents a manufacturer’s confidence in how close the measurement is to the actual value. (The previous section introduced this idea.) Intuitively we understand this because even after identifying all the sources of error and making needed adjustments, there is still uncertainty about the reliability of the measured value.
It is interesting to note that in the example uncertainty calculation by NIST given below, one of the components of combined uncertainty in their model includes errors due to creep, hysteresis, loading angle and similar factors. All of these mitigate with proper measurement methods and calibration. Therefore the final combined uncertainty figure in [5] is actually given as a best case and worst case range, when these factors are, and are not mitigated.
Standards Procedures for Estimating Measurement Uncertainty
This section explains the general steps followed in evaluating measurement uncertainty in accordance with OIML’s Guide to the Expression of Uncertainty in Measurement (GUM) standard [1].
1. Modeling the Measurement
To understand this step, it is important to understand that force measurement is not a direct measurement. An example of a direct measurement is determining the width of a pipe with calipers. The measuring system bases its reading on the actual width of the pipe. An indirect measurement is one where the measuring system translates an input to a different form of output. An example of this the conversion of the exerted force on a load cell to electrical energy, which a display device then “reads” and converts to a number. Each conversion introduces additional uncertainty in the measurement.
Understanding the Components of a Measurement
Modeling the measurement is simply a way of mathematically representing this relationship between the output of a measuring system, \(Y\) and the input quantities \(X_{i}\). This notation of upper case and lower case variables distinguishes the actual value (upper case) which, recall, is always truly unknown, with its best estimate (lower case). Since measurements are a best estimate of an actual value, they appear in the expression below as lower case values (\(x_{1}, x_{2},…, x_{N}\)). Likewise, since the output estimate is a function of all of the input measurements, it appears in the expression below as lower case \(y\). The relationship between the output and inputs of a measuring system is then:
\(y=f(x_{1},x_{2},…,x_{N})\)
The important thing to understand about this is simply that, since the output estimate is a function of estimates for the inputs, and that each input estimate has a level of uncertainty associated with its value, these input uncertainties cumulatively determine the combined standard uncertainty associated with the output of the measuring system, denoted as \(u_c(y)\). That is, the components of a measurement determine its components of uncertainty.
Understanding the Combined Standard Uncertainty Model
NIST calculates combined standard uncertainty as a function of the uncertainties due to the applied force, the display, and the device’s response [5]. In turn each of these uncertainties have their own components of uncertainty. For example, uncertainty in dead weight mass, acceleration due to gravity and air density all compose the uncertainty due to applied force.
More specifically, the sources of combined uncertainty (denoted \(u_c\)) considered to be attributable to the transducer force measurement are the applied force (denoted \(u_f\)), the calibration of the indicating instrumentation (denoted \(u_v\)), and the fit of the measured data to the model equation (denoted \(u_r\)).
Because the combined standard uncertainty is a function of the uncertainties due to these three factors, NIST expresses this relationship as:
\(u_{c}^2= u_{f}^2 + u_{v}^2 + u_{r}^2\)
The standard combined uncertainty is simply the square root of either side of this equation. The 95% confidence interval is this number times a coverage factor of 2. The 99.7% confidence interval is this number times a coverage factor of 3.
Each of these components of uncertainty on the right side of the equation above also have their own components of uncertainty, like the proverbial layers of an onion. We will address how to obtain these figures later in this document, applying OIML recommendations.
2. Evaluating the Standard Uncertainty of Each Input Quantity
The standard uncertainty of each input estimate (\(u(x_{i})\)) is itself a standard deviation of the mean, or multiple thereof, given a distribution of possible values for the true or actual inputs (\(X_{i}\)).
There are two methods of evaluating the standard uncertainty [7], assuming multiple types of distributions for the possible true input values. In the first method, the distribution of output values is from actual measurement data; in the second, the distribution of output values is theoretical.
Type A Evaluation:
This method involves performing a series of repeated measurements of the inputs. It involves calculating the mean of all the samples \(n\) representing their total quantity), calculating the experimental standard deviation (the square root of the sum of squared differences between each sample and the mean) and finally calculating the standard deviation of the mean. The standard deviation of the mean is what the standard uncertainty becomes. The illustration below should explains in greater detail.
Mean
Standard Deviation
Standard Deviation of Mean
Type B Evaluation:
This method involves determining the standard uncertainty with existing information about possible true inputs. It clearly states the assumptions of the uncertainty sources and their values. These values may come from the calibration certificate, authoritatively published quantity values, certified reference materials and handbooks, or personal experiences and general knowledge of the instrument. This method is ideal when taking measurements repeatedly is impractical (e.g., due to cost or time constraints).
Type B evaluation relies on the triangle and rectangular distributions. By contrast, Type A evaluation uses the normal distribution. Figure 1 below shows these distributions and their functions; in each “\(a\)” is the upper and lower bound of possible values; \(u(X)\) is the uncertainty around the expected value (which is the midpoint of a distribution curve).
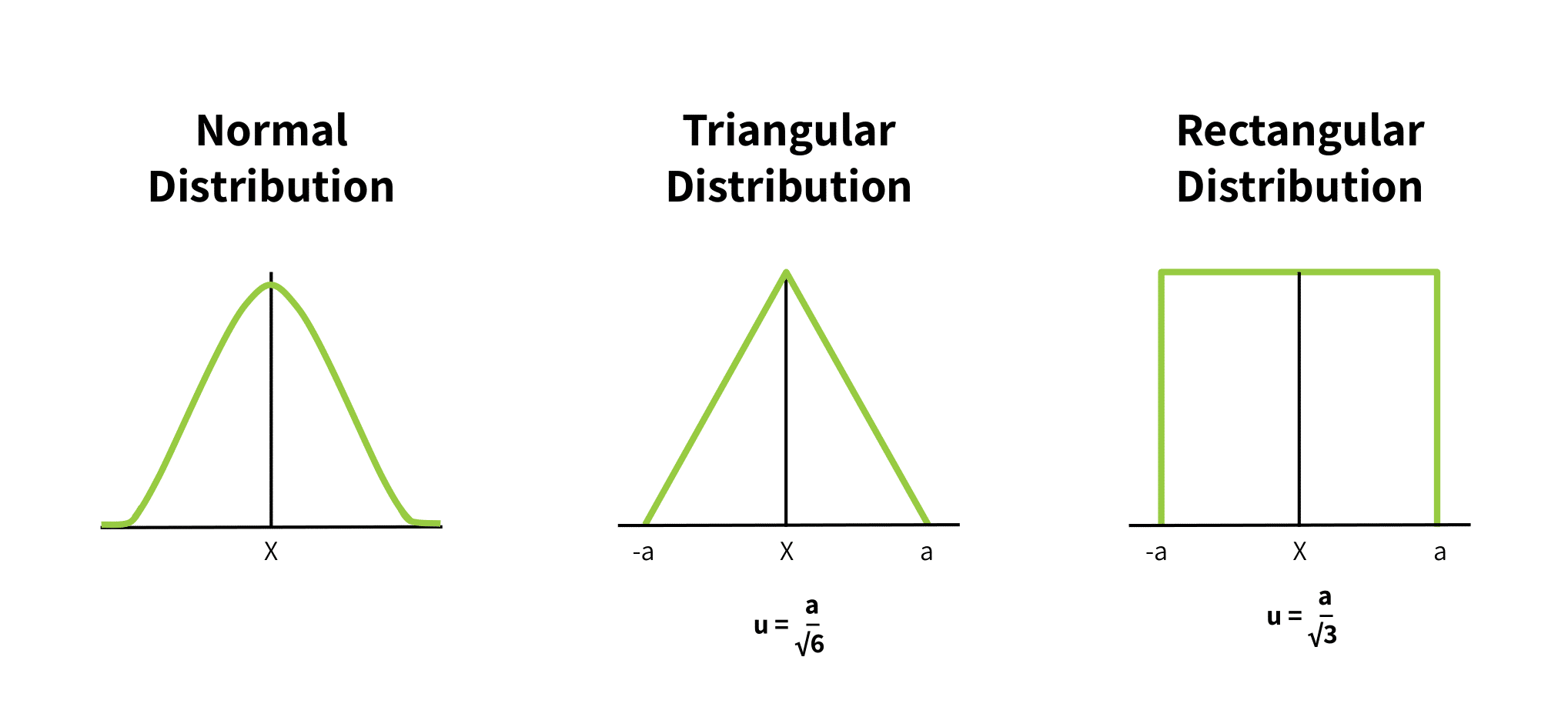
Clearly the normal distribution gives the best picture of uncertainty. However, this involves costly and time consuming experimentation.
A rectangular distribution is appropriate when a given uncertainty does not include a confidence interval. Instead the calculation assumes that all values of the input will fall into a range of values with equal probability. While this is an oversimplification, this assumption gives a valid highest bound of uncertainty, expressed by the equation below the distribution.
A triangular distribution is appropriate when the model of possible true inputs should reflect that values close to the mean are most possible, and the probability of values declines as they get further from the mean. It is an approximation of a normal distribution in the absence of actual measurements. The equation for the standard uncertainty for this assumed distribution appears below the figure.
3. Determining the Combined Standard Uncertainty
The most commonly used method for this is the GUM’s law of propagation of uncertainty (LPU). LPU involves the expansion of the mathematical model in a Taylor series and simplifying based on only the first order terms.
The combined standard uncertainty is simply the appropriate combination of standard uncertainties for each input quantity in step 2. The right expression for the combined standard uncertainty depends on whether the input quantities are independently or interdependently correlated. If they are independent, the expression is:
\(u_{c}^{2}(y)=\sum_{i=1}^{N}\left [ \frac{\partial f}{\partial x_{i}} \right ]\)
If they are interdependent, the expression below is added to the right-hand side of the one above:
\(\sum {i=1}^{N}\sum {j=1}^{N}\left [ \frac{1}{2} \left [ \frac{\partial^{2} f}{\partial x_{i}\partial x_{j}} \right ]^{2}+\frac{\partial f}{\partial x_{i}}\frac{\partial ^{3}f}{\partial x_{i}\partial^{2} {x{j}}}\right ]u^{2}(x_{i})u^{2}(x_{j})\)
In the equation above, the partial derivatives are called the sensitivity coefficients. Each of these coefficients is the standard uncertainty of the i-th input quantity. The unsquared value of the product of the partial derivatives with the standard uncertainty is called the uncertainty component.
4. Determining the Expanded Uncertainty
The expanded uncertainty widens the confidence interval of an expected measurement result. Denoted by \(U\), it equals the combined standard uncertainty multiplied by an integer known as the coverage factor, \(K\). Expanded uncertainty ensures the result encompasses a large portion of the distributed values reasonably attributable to the measurand. Mathematically it is:
\(U=Ku_{c}(y)\)
Therefore, the measurement result can be expressed conveniently as \(Y = y\pm{U}\). That is, \((y-U)\leq{Y}\leq(y+U)\). Recall the example of the FSO taken to be as \(2.2 mV/V \pm0.005 mV/V\).
A coverage factor of two gives a confidence interval for the uncertainty of about 95%. Similarly a coverage factor of three gives a confidence interval of uncertainty of about 99.7%. This means the results will fall within the mean result \(\pm{U}\) about 95% or 99.7% of the time respectively.
Lab Procedures for Determining Force Measurement Uncertainty
The above are internationally accepted procedures for calculating any measurement uncertainty, per OIML documentation. This section gives an example of how these general procedures are applied in a real life laboratory, in this case the procedures used by NIST to calibrate their own testing equipment and certify manufacturer’s load cells [5].
1. Modeling the Measurement
The polynomial equation that models the force transducer response is:
\(R=A_{0}+ \sum A_{i}F^{i}\)
Where R is the response, F is the applied force and the \(A_{i}\) is the coefficient calculated by applying the least-square fit method to the data set. This equation will become most relevant in step 2 below when we model its uncertainty, which is the third factor (\(u_{r}^2\)) of the combined standard uncertainty above.
2. Evaluating the Standard Uncertainty of Each Input Quantity
The Uncertainty in Applied Force
The components most significantly contributing to the uncertainty of the applied force (\(u_f\)) are threefold. The uncertainty in the dead weights themselves are one factor. This is because, again, it is impossible to know the true weight of any entity. The remaining factors contributing to applied force uncertainty are the uncertainty in the acceleration due to gravity at the altitude of the test (since force is a function of the mass and gravitational acceleration, or as we learn in high school physics, \(F=ma\)), and the air density at the specific location. These factors may seem minuscule but for very precise systems they are significant and imperative to account for.
The standard uncertainty of the applied force, is then modeled by the equation:
\(u_{f}^{2}=u_{fa}^{2}+u_{fb}^{2}+u_{fc}^{2}\)
where \(u_{fa}\) is the standard uncertainty associated with the mass, \(u_{fb}\) is the acceleration due to gravity, and \(u_{fc}\) is the standard uncertainty due to air density. The value of \(u_{f}^{2}\) is substituted in the combined standard uncertainty equation in step 3 below.
Each of these quantities has been determined by NIST through Type A evaluation for their specific lab location, and can be found in [5].
The Uncertainty of The Voltage Ratio Instrumentation
Recall that force measurement is an indirect measurement. This means the displayed weight is an interpretation of a transducer’s output voltage transducer. (It is not, by contrast, a comparison with a known weight on a balance scale.) This inherently introduces error, since the display or other indicating instrument has its own associated uncertainty.
NIST includes the following standard uncertainty sources in this figure:
- The calibration factor of the multimeter, denoted as \(u_{va}\); this is the ratio of the mutimeter’s display voltage to that of a reference voltage
- The uncertainty associated with the multimeter’s linearity and resolution, denoted as \(u_{vb}\), that affects its least square fit to a model curve.
- The uncertainty associated with the results of the primary calibration of the multimeter using a primary transfer standard such as a precision load cell simulator, denoted as \(u_{vc}\).
In total, the standard uncertainty \(u_{v}\) associated with the instrument is a combination of its sources
\(u_{v}^{2}=u_{va}^{2}+u_{vb}^{2}+u_{vc}^{2}\)
The value of \(u_{v}^{2}\) becomes the second term in the combined standard uncertainty equation in step 3 below. Its value has been derived by NIST using Type A evaluation in their laboratory and can be found in [5].
The Uncertainty Due to the Deviation of the Observed Data from the Fitted Curve
Step 1 above showed that the polynomial equation modeling the force transducer response was:
\(R=A_{0}+ \sum A_{i}F^{i}\)
This equation models what we expect the output of the tested transducer to look like; it is a theoretical model taking into account its electrical components. However, the actual readings from the transducer will deviate from this curve for various applied forces. The differences between the theoretical and measured values for a given input create the standard uncertainty of the response, denoted as \(u_{r}\) and calculated as:
\(u_{r}^{2}=(\sum d_{j}^{: 2})/(n-m)\)
Where \(d_{j}\) are the differences between the measured response \(R_{j}\) and those calculated using the model equation, \(n\) is the number of individual measurements in the calibration data set, and \(m\) is the order of the polynomial modeling the theoretical output, plus one.
The value of \(u_{r}^{2}\) becomes the third term in the combined standard uncertainty equation in step 3 below. Again, its value has been derived by NIST using Type A evaluation in their laboratory and can be found in [5].
3. Determining the Combined Standard Uncertainty
Recall from earlier in this document, the combined standard uncertainty is:
\(u_{c}^{: 2}=u_{f}^{: 2}+u_{v}^{: 2}+u_{r}^{: 2}\)
The terms derived in step 2 are placed in this equation, and the combined standard uncertainty, \(u_{c}\), is calculated by taking the square root of each side.
4. Determining the Expanded Uncertainty
Again recall from before, the expanded uncertainty \(U\) is the product of the combined uncertainty \(U_{c}\) and the coverage factor, \(K\). For NIST’s desired confidence interval of 95%, the value of \(K\) is 2, and the expanded uncertainty is therefore:
\(U=Ku_{c}=2u_{c}\).
The Importance of Determining Force Measurement Uncertainty
We’ve covered how to determine measurement uncertainty. The question is then “why do it?” The following points express the importance of quantifying the uncertainty in force measurements with rigor.
1.
The uncertainty value of a force measurement provides a benchmark to compare one’s measurement results with those obtained in other laboratories or by national standards.
2.
It helps to properly interpret the results obtained under different conditions. For example, calibration maybe performed under laboratory conditions, while the measurement using the force transducer maybe under totally different conditions. Consequently, there will be differences in the results. These conditions can be grouped into geometrical, mechanical, temporal, electrical, and environmental effects [4]. Accounting for these differences is in the expression of the uncertainty of each result.
3.
The results of the evaluation of a measurement device’s uncertainty can serve as a statement of compliance to requirements, if a customer or regulation requires such a statement.
4.
Uncertainty testing is a means of determining the capability of the force measurement system to provide accurate measurement results.
5.
Specifically, the uncertainty components that form the combined uncertainty value can help pinpoint the measurement variables needing improvement.
6.
Understanding the principles of measurement uncertainty used by a laboratory, along with practical experiences, can improve methods of force measurement.
7.
The principles of evaluating force measurement uncertainty can help maintain and improve product quality and quality assurance.
Conclusion
Measurement uncertainty is an important concept to understand when selecting and also when calibrating and maintaining load cells. Whereas load cell specification sheets give values of uncertainty, they do not explain their derivation. This article explains globally accepted standard procedures for calculating measurement uncertainty.
As stated before, proper measuring technique and load cell design can lessen the significance of the uncertainty components modeled above. For example proper axial loading, the load cell measurement resolution, the ability to reduce unwanted noise, and the repeatability of the display results all contribute to the deviations in the response vs. the theoretical response curve. Moreover, hysteresis and creep contribute greatly to the uncertainty of the response, \(u_r\), but are controllable with proper maintenance and calibration. (See Calibrating the Force Measuring System and Quality Control: Load Cell Handling, Storage and Preservation Dos and Don’ts.)
In practice, manufacturers design to given, accepted tolerances for a particular class of load cells. (See Load Cell Classes: NIST Requirements and Significant Digit Considerations for Weighing Applications.) Then they specify a load cell measuring range or range of forces that is narrower than the true maximum and minimum capabilities of the load cell. Deviations from expected measurement values are generally more extreme at the limits of the measuring range. Therefore the narrower range ensures the potential errors are well within the bounds of the load cell’s specified tolerances.
References
[1]
Joint Committee on Guides in Metrology (JCGM), “Evaluation of Measurement Data – Guide to the Expression of Uncertainty in Measurement,” JCGM, 2008.
[2]
Joint Committee for Guides in Metrology (JCGM), “JCGM 200:2008 International vocabulary of metrology – Basic and general concepts and associated terms (VIM),” Joint Committee for Guides in Metrology, 2008.
[3]
A. G. Piyal Aravinna, “Basic Concepts of Measurement Uncertainty,” 2018.
[4]
Dirk Röske, Jussi Ala-Hiiro, Andy Knott, Nieves Medina, Petr Kaspar, Mikołaj Woźniak, “Tools for uncertainty calculations in force measurement,” ACTA IMEKO, vol. 6, pp. 59-63, 2017.
[5]
Thomas W. Bartel, “Uncertainty in NIST Force Measurements,” Journal of Research of the National Institute of Standards and Technology, vol. 110, no. 6, pp. 589-603, 2005.
[6]
European Association of National Metrology Institutes (EURAMET), “Uncertainty of Force Measurements,” 2011.
[7]
Jailton Carreteiro Damasceno and Paulo R.G. Couto, “Methods for Evaluation of Measurement Uncertainty,” IntechOpen, 2018.
[8]
NIST Handbook 44, “Specifications, Tolerances and Other Technical Requirements for Weighing and Measuring Devices,” Appendix A, “Fundamental Considerations,” 2018 Edition



