
The minimum weight measurable by a load cell is important knowledge when designing a load measurement application. Likewise, determining the load cell resolution, or smallest change in weight the load cell can detect, is equally important. This article explains how to uncover these critical pieces of information.
However, these aren’t the only considerations when determining the resolution of the entire weighing system. This article expands on these other factors as well.
The Most Important Data Sheet Specifications: Divisions and Full Scale Output
Every strain gauge load cell comes with a data sheet with a list of its specifications. One such specification is the number of divisions. The divisions are simply the number of increments a load cell’s full scale output (FSO) voltage can be divided into. Requirements bodies such as OIML (internationally) and NIST (in the US) determine what is known as the accuracy class of a load cell by its number of divisions. The articles, Load Cell Classes: OIML Requirements and Load Cell Classes: NIST Requirements go into more depth with this topic. A load cell certified to adhere to one of these sets of requirements will have a marking indicating compliance; this compliance implies adherence to a set of performance tolerances associated with each accuracy class.
Because the FSO reflects the range of voltages from zero to maximum load per volt of excitation power, one can assume that the number of divisions is also the number of increments from the minimum load to maximum load. (Figure 1 expresses this relationship.) Therefore, the smallest weight accurately measurable by the load cell is simply the maximum measuring range divided by the number of divisions.
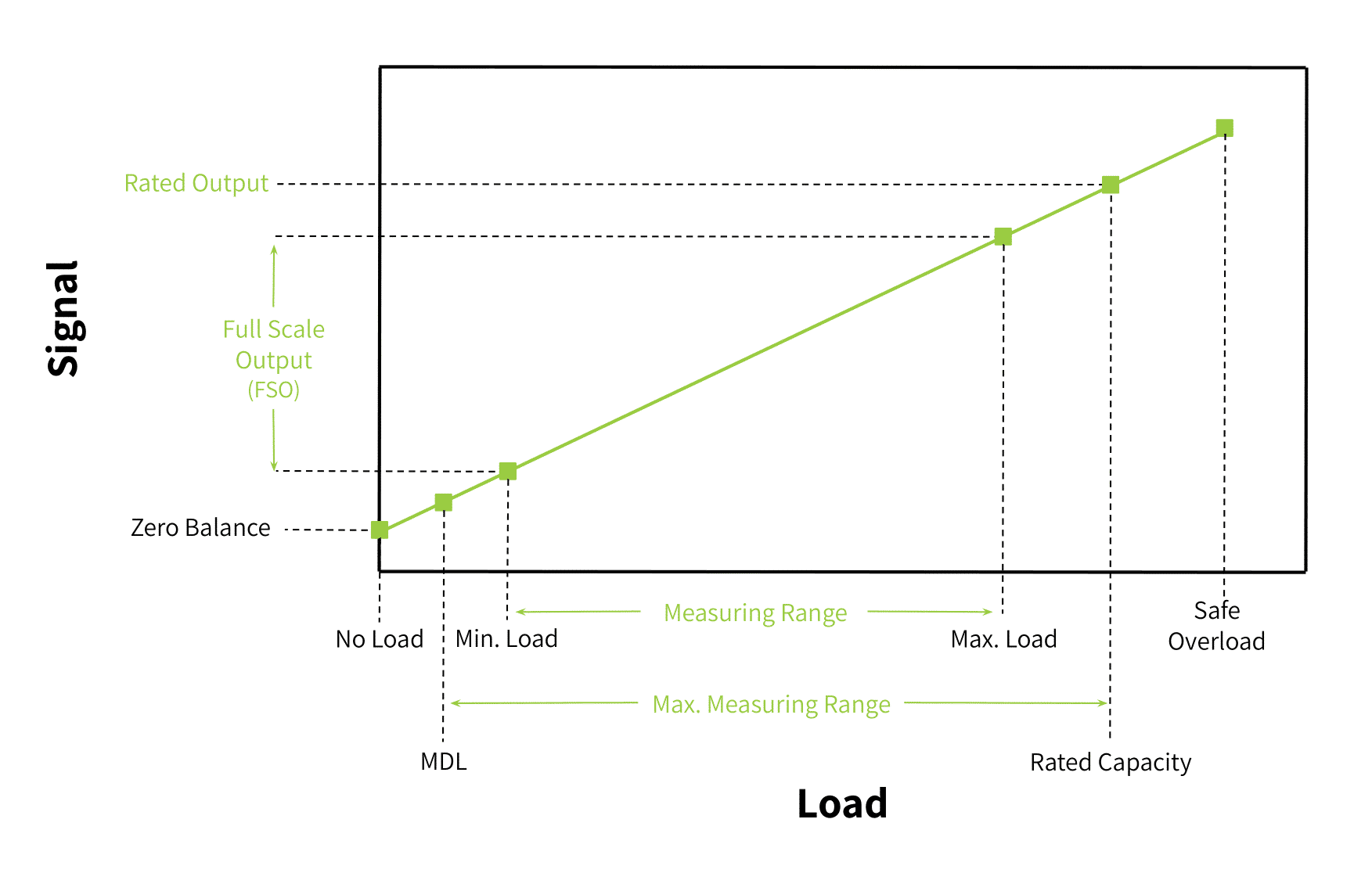
Figure 1: Terms Associated With Loads Applied to Load Cells, and Their Relationship
However, weighing systems are not just load cells. Signal conditioners and displays are also part of the system. In determining the resolution of a weighing system, one must also consider the capabilities of these components. The next sections discuss these issues.
The Scale Display’s Resolution: How it Affects Minimum Weight
A display’s input sensitivity is the smallest signal, or change in signal, that it can detect. The output of the load cell per smallest measurable unit of weight must therefore be greater than the input sensitivity of the display. Otherwise, the measuring system will not give an accurate result.
For example, assume you have a scale whose internal load cell has a maximum load of 50lbs, a FSO of 1mV/V, and a recommended excitation voltage of 10V. Assuming the recommended excitation of 10mv; this means the load cell will output 10mV (1mV/V \(\times\) 10V) to the display when it bears the maximum of 50lbs.
Let’s assume this load cell has 8000 divisions. In other words, it can measure a weight as small as a tenth of an ounce (0.00625lbs). The output voltage at this weight can be calculated as follows (since the relationship is linear):
\begin{align*}
\frac{0.00625 \text{lbs}}{50 \text{lbs}} &= \frac{X mV}{10 mV} \ \
\begin{split}
\text{therefore, } X &= 10 mV \times \frac{0.00625}{50} \\
&= 0.00125 mV, \text{ or }1.25 \mu{V}
\end{split}
\end{align*}
The input sensitivity of the display must therefore be lower than \(1.25 \mu{V}\); otherwise a weight of \(t\frac{1}{10} oz\) will not give a readout. Likewise any tenth of an ounce increment of a larger weight will not display. Therefore, the lowest weight detectable by a load cell is clearly not the only consideration in designing a weighing system.
Note that most displays are able to handle a small input signal such as this one. This is because they generally have internal amplifiers. The next section explains the effects of amplifiers on the resolution of the overall weighing system. Unlike this section, it also covers resolution issues associated with digital signal converters.
Signal Amplification
Typically the load cell output signal undergoes signal amplification. This process boosts the output signal to a detectable level. An instrumentation amplifier is common. This amplifier uses two input buffers for high input impedance; it also has a difference amplifier between the load cell output and the analog-digital converter (ADC). The ADC takes an analog signal and converts it into a discrete signal usable by a digital display.
Figure 2 shows a standard instrumentation amplifier circuit.
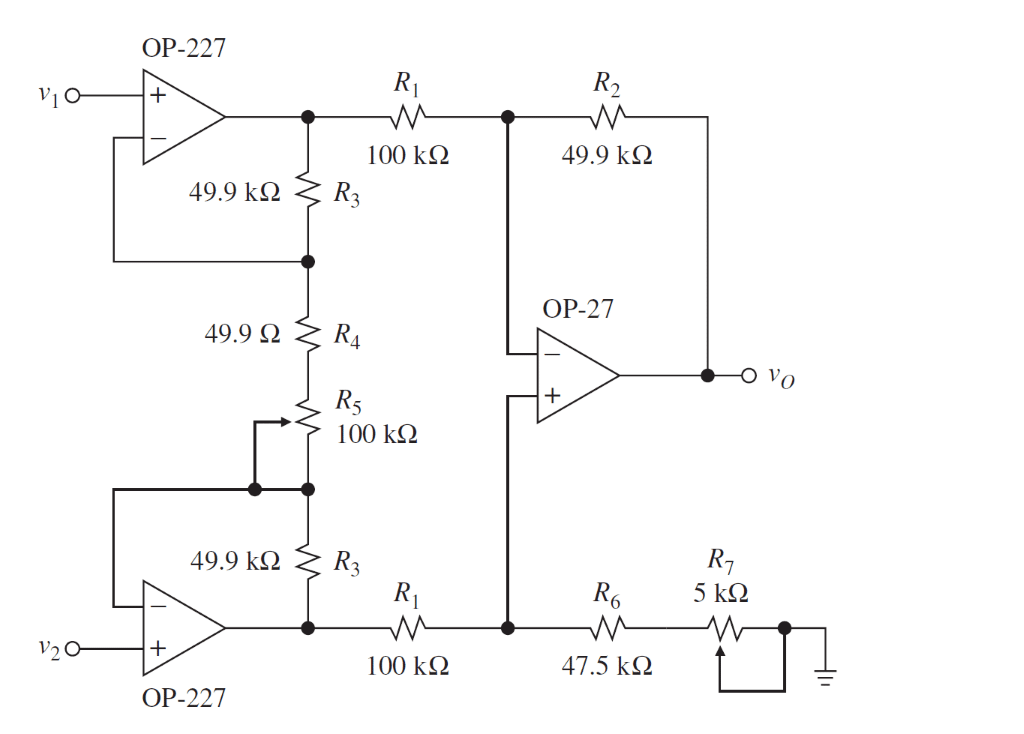
Figure 2: Instrumentation Amplifier
The instrumentation amplifier stage needs to have high differential gain, high power supply rejection ratio, low drift, low offset and low input bias current [2]. If it has all of these qualifications, the amplifier’s signal-to-noise ratio will be large enough for the ADC to accurately digitize the signal.
A direct correlation exists between the number of divisions of the ADC and the load cell’s number of divisions. An ADC must have high enough resolution (i.e. enough bits) to detect small changes from a high division load cell. Load cell indicator manufacturers generally provide the ADC’s required number of bits; occasionally they even recommend which load cells to use with the system.
Other Load Cell Specifications That Affect A Weighing System’s Resolution
The load cell’s divisions, along with the amplifier’s and display’s respective capabilities to detect a low signal clearly affect the weighing system’s resolution. However, the reliability of these measurements is only as good as the quality of the load cell itself. A few of its specifications tell us its error tolerances under certain ambient conditions. For applications requiring high accuracy, you will want these tolerances to be as low as possible. The reason for this is that the tolerances are given as a percentage of full scale measurements; therefore one can see how this value can be a large percentage of a small measurement increment. Likewise for high-accuracy applications, you will want a load cell with a higher level of sensitivity.
Figure 3 displays typical specifications found on a load cell data sheet. They are explained further in this section. More information appears in these articles: How to Read A Load Cell Datasheet and Load Cell Classes: NIST Requirements.
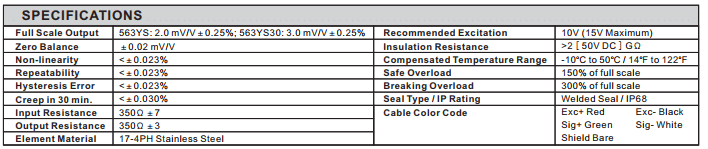
Figure 3: Specifications from a Load Cell Data Sheet
Maximum Error
As seen in Figure 3, load cell specifications include error ranges for various causes such as non-linearity, hysteresis and creep. The sections below further define these terms. The sum total of these errors is known as the combined error or maximum possible error. The maximum possible error is important when considering accurate division measurements [3]. If a load cell experiences its maximum possible error, its minimum weight divisions be less reliable. A load cell with a 0.1% combined error is accurate to a maximum error of ±0.1% of rated output. This means the total error could be very high compared to a single increment of measurable weight.
The total error is determined by a number of varying factors, from temperature deviations to magnetic interference. The following definitions are important determinants of the accuracy class of a load cell. Understanding the source of error can help increase accuracy when testing a load cell system. These definitions are provided from the Handbook of Electronic Weighting.
Non-Linearity
This expresses the maximum deviation of the calibration curve. To create this curve, one gradually increases the applied weight from the zero balance level to the rated output of the load cell, and plots the output vs this weight. The smaller the non-linearity, the more accurate measurement we obtain.
Hysteresis
This is the maximum deviation of an output signal for the same load. One obtains the first set of values are by increasing the applied weight from zero balance to the rated output; likewise, the second readings are obtained by decreasing the rated output to the zero balance level. Assume the x-axis is the applied weight and the y-axis is the output on a plot. The smaller this difference in y values (output) at a single x value (weight), the more accurate measurement we obtain.
Creep
This specification becomes very important when a load is constant over a long time, such as for monitoring purposes. Creep is the change in the load cell output signal over time under a constant load, with unchanging environmental conditions.
Repeatability
This is the maximum difference in the load cell’s output signal for repeated identical loads under identical environmental conditions. A small value depicts a high system accuracy and reliability.
Temperature Effect on Output
This describes the effect of temperature changes on the output of the load cell. Temperature changes alter the resistance of the gauges and can introduce errors that affect system accuracy. Note the compensated temperature range in the specification sheet. Maintaining this ambient temperature in the weigh system’s operating environment will ensure the load cell operates within its specified tolerances.
Summary
As this article explains, several important load cell specifications give clues to the minimum weight it can measure. The number of divisions and range of weight determine a load cell’s minimum weight that is accurately detectable.
Note that if the cell is not designed for such operation, its resulting accuracy and precision might not be great, but it will still produce a measurement. This FAQ question and answer address this case. The other load cell specifications will indicate the total error of the load cell. This is important to know since the error could be a very large percentage of a very small weight increment.
Since every application is different, contact Tacuna Systems should you have any questions about the resolution of our load cells in your weighing system.
Sources
- Brusamarello, V., Machado de Brito, R., Muller, I., Pereira, C. E., “Load Cells in Force Sensing Analysis – Theory and a Novel Application”, ResearchGate, Jan. 2010.
- Franco, S. “Design with operational amplifiers and analog integrated circuits”. New York: McGraw-Hill. pp. 87, 2015
- K. Elis Nordon, “Handbook of Electronic Weighting”, Wiley-VCH, pp. 24-29, Jul. 1998.
- “Load Cell Accuracy in Relation to the Conditions of Use”, Technical Note VPGT-02, Jan. 8 2015. Retrieved from http://www.vishaypg.com/docs/11864/11864.pdf
- “Load Cell and Weight Module Handbook”, Rice Lake Weighing Systems, pp. 9-10, 2010
- “OIML Certificate of Conformity”, Number R60/2000-NL1-10.27 , Dec. 2010
- “R 60 OIML-CS rev.2”, NIST Handbook 44, pp. 1-4, Jan 5 2018.



